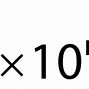
Aturan Angka Penting Dalam Perkalian

Perkalian dan Pembagian

Penulisan jumlah angka penting hasil perkalian atau pembagian sama dengan jumlah angka penting paling sedikit dari bilangan-bilangan yang dioperasikan. Misalnya, hasil perkalian antara 1,6283 cm (4 angka penting) dengan 2,2 cm (2 angka penting) adalah 1,8226 cm. Maka, hasil akhirnya harus dituliskan menjadi 1,8 cm (2 angka penting).

Sementara itu, perkalian angka antara hasil pengukuran dengan hasil membilang, hasil akhirnya harus mempunyai jumlah angka penting paling sedikit yang sama dengan angka penting pada hasil pengukuran.

Misalnya, keramik lantai mempunyai panjang 50,25 cm dan lebar 20,1 cm (panjang dan lebar adalah angka dari hasil pengukuran). Apabila terdapat 25 buah keramik (jumlah angka dari hasil membilang) yang digunakan untuk menutup lantai, maka berapakah luas lantai yang tertutup keramik?

-   Panjang = 50,25 cm (4 angka penting), lebar = 20,1 cm (3 angka penting), dan jumlah keramik = 25 keramik (dua angka penting).

-   Untuk mengukur luas lantai = panjang x lebar x jumlah keramik = 50,25 x 20,1 x 25 = 25.250,625 cm2.

-   Maka, hasil akhirnya harus ditulis 25.200 atau 2,52 x 104 cm2 (3 angka penting).

Dalam menuliskan angka penting tersebut berlaku aturan pembulatan angka 5. Jika sebelum angka 5 terdapat bilangan ganjil, maka dibulatkan ke atas. Sementara apabila sebelum angka 5 terdapat bilangan genap, maka angka 5 dihilangkan. Misalnya, 2,25 menjadi 2,2 dan 2,35 menjadi 2,4.

Jumlah angka penting dari hasil perhitungan pangkat atau akar harus mempunyai jumlah angka penting yang sama dengan yang dioperasikan. Misalnya:

-   Akar dari 2,25 adalah 1,5, lalu ditulis menjadi 1,50.

-   Pangkat dua dari 2,5 adalah 6,25, lalu ditulis menjadi 6,2 (berlaku aturan pembulatan angka 5).

KOMPAS.com – Dalam suatu bilangan, tidak semua angka merupakan angka penting. Apa yang dimaksud dengan angka penting? Berikut adalah pengertian, aturan, dan contohnya!

Setiap angka nol di akhir tanpa titik desimal bukan angka penting

Dilansir dari Lumen Learning, setiap angka nol di akhir tanpa titik desimal hanya berfungsi untuk menempatkan angka penting di posisi yang benar dan bukan merupakan angka penting.

Misalnya, bilangan 12.000 yang hanya memiliki dua angka penting yaitu 1 dan 2.

Baca juga: Bentuk Desimal dari 27/25 dan 3/8

Penjumlahan dan Pengurangan

Angka hasil penjumlahan atau pengurangan hanya boleh dituliskan satu angka taksiran. Misalnya, hasil penjumlahan 3,219 cm; 15,5 cm; dan 8,43 cm adalah 27,149 cm. Maka, hasil akhirnya harus dituliskan menjadi 27,1 cm, sehingga hanya memiliki satu angka taksiran.

Rumus Excel Penting Diketahui: Pengurangan, Perkalian, Penjumlahan

- Banyak tas yang dimiliki Tasya ada 3. Tasya dapat memilih salah satu dari 3 tas tersebut.

Setiap angka nol di depan tanda desimal bukan angka penting

Jika setiap angka nol di belakang tanda desimal adalah angka penting. Maka, setiap angka nol di depan tanda desimal dan angka bukan nol bukanlah angka penting.

Misalnya, bilangan 0,2 yang hanya memiliki satu angka penting yaitu 2.

Sonora.ID - Dalam artikel ini kita akan mempelajari bersama mengenai salah satu materi Fisika, yakni angka penting.

Apa sih yang dimaksud dengan angka penting itu? Berikut ini penjelasan lengkapnya mengenai pengertian, aturan, dan pembulatan angka penting yang dikutip dari buku Fisika 1A.

Pengertian Angka Penting

Angka penting disebut juga angka berarti atau angka signifikan, yaitu angka yang menunjukkan ketelitian

atau ketidakpastian alat ukur yang digunakan.

Angka penting ini diperoleh dari hasil pengukuran. Sementara itu, angka yang bukan berasal dari hasil pengukuran disebut angka eksak, misalnya, jumlah siswa dalam satu kelas 30 orang.

Semakin banyak angka penting dalam suatu hasil pengukuran, semakin telitilah alat ukurnya. Contohnya, panjang rusuk kubus menurut jangka sorong adalah 13,4 mm dan menurut mikrometer sekrup 13,45 mm.

Bilangan 13,4 terdiri atas 3 angka penting; bilangan 13,45 terdiri atas 4 angka penting.

Angka penting terdiri dari angka pasti dan angka taksiran (angka perkiraan atau angka diragukan). Misalnya, pada pembacaan panjang rusuk kubus dengan menggunakan mistar diperoleh angka 13,4 cm.

Angka 1 dan 3 adalah angka pasti karena jelas terdapat pada skala. Angka 4 diperoleh dari perkiraan sehingga disebut angka perkiraan atau angka diragukan.

Angka perkiraan selalu berada pada posisi terakhir atau diberi tanda khusus (misalnya, garis bawah atau dicetak tebal). Di belakang angka perkiraan, bukan angka penting lagi dan tidak mempunyai arti.

Baca Juga: Rumus Usaha dalam Fisika: Contoh Soal Lengkap dengan Jawabannya

Sebuah angka adalah angka penting atau bukan dapat dilihat pada aturan di bawah ini.

Pembulatan Angka Penting

Aturan pembulatan angka penting adalah sebagai berikut.

Aturan Berhitung dengan Angka Penting

(1) Penjumlahan dan pengurangan

Hasil penjumlahan dan pengurangan angka penting hanya boleh mengandung satu angka perkiraan. (Angka yang diragukan/perkiraan dicetak tebal).

62,4 m + 15,32 m = 77,72 m = 77,7 m.

(2) Perkalian dan pembagian angka penting dengan angka penting

Hasil perkalian dan pembagian angka penting sama dengan banyaknya angka penting dari bilangan yang memiliki angka penting paling sedikit.

Misalnya, 2,32 cm x 2,8 cm = 6,496 cm² = 6,5 cm²

Jika terjadi perkalian berturut-turut, dua bilangan dikalikan dan dibulatkan dulu, lalu dikalikan dengan bilangan ketiga.

2,32 m x 2,4 m x 1 ,73 m=.....

2,32 m x  2,4 m= 5,568 m² = 5,6 m²

5,6 m² x 1,73 m= 9,688 m³

Hasil akhirnya menjadi 9,7 m³.

(3) Perkalian atau pembagian antara angka penting dengan angka eksak

Hasil perkalian atau pembagian antara angka penting dengan angka eksak memiliki angka penting sebanyak yang dimiliki angka pentingnya.

Misalnya, panjang sebatang kapur 4,67 cm (angka penting). Jika 12 buah kapur (angka eksak) saling disambungkan, panjangnya adalah 56,0 cm. Ini diperoleh dari 4,67 cm x 12 = 56,04 cm = 56,0 cm (3 angka penting).

(4) Pemangkatan dan penarikan akar

Banyaknya angka penting hasil pemangkatan dan penarikan akar sama dengan bilangan yang dipangkatkan atau ditarik akarnya.

Misalnya: 5,0 cm³ = 125cm³ = 130 cm³ (2 angka penting)

∛125m³ = 5,00 m (3 angka penting).

Demikianlah paparan lengkap mengenai materi angka penting.

Baca Juga: Cara Menghitung Mikrometer Sekrup yang Paling Tepat dan Benar

Baca berita update lainnya dari Sonora.id di Google News.

13 Desember 2024 22:30 WIB

13 Desember 2024 18:57 WIB

13 Desember 2024 18:20 WIB

13 Desember 2024 18:15 WIB

0%0% found this document useful, Mark this document as useful

0%0% found this document not useful, Mark this document as not useful

JAKARTA, iNews.id - Contoh soal aturan perkalian berikut patut dipelajari. Aturan perkalian merupakan salah satu konsep dasar matematika yang penting untuk dikuasai.

Konsep ini membantu siswa memahami berbagai situasi di mana dua kejadian independen terjadi secara bersamaan. Untuk mengukur kemampuan siswa dalam memahami materi mengenai aturan perkalian, soal-soal berikut dapat dikerjakan.

Contoh Soal Aturan Perkalian

1. Tasya mempunyai 3 tas dan 2 sepatu. Pada saat akan bepergian, Tasya memakai salah satu dari tas dan sepatu. Ada berapa pilihan yang dapat dipakai Tasya?

Rumus Perkalian di Microsoft Excel yang Paling Mudah

Plat nomor boleh ada angka yang sama, artinya angka yang sudah dipakai boleh dipakai lagi.

Kita buat 4 kota karena plat nomor terdiri dari 4 angka saja. Pilihan angkarnya adalah 1, 2, 3, 4, 5, artinya totalnya ada 5 pilihan angka. Cara pengisian setiap kotak:

- Kotak I, dapat diisi angka 1, 2, 3, 4, atau 5 sehingga ada 5 cara.

- Kotak II, dapat diisi dengan 5 pilihan angka juga karena angka yang sudah dipakai pada kotak I bisa dipakai lagi pada kotak II.

- Begitu juga dengan kotak III dan kotak IV ada 5 pilihan angka masing-masing. Banyaknya plat nomor = 5 × 5 × 5 × 5 = 625.

Jadi, banyaknya plat nomor yang bisa dibuat adalah 625 plat nomor.

3. Rahma mempunyai 6 buah kaus, 5 buah kemeja dan 4 buah celana panjang. Tentukan banyaknya variasi pakaian yang dapat dipakai Rahma?

Rahma dapat memakai kaus, kemeja, dan celana panjang secara bersamaan.

Jadi, dengan aturan perkalian banyak variasi pakaian yang dapat dipakai Rahma andra adalah:

Kaidah Pencacahan (Aturan Penjumlahan dan Aturan Perkalian

4. Suatu menu makan siang terdiri dari sayur, lauk, buah dan minuman masing-masing satu macam. Jika terdapat 3 macam sayur, 4 macam lauk, 5 macam buah dan 3 macam minuman. Berapakah banyaknya menu makan siang yang dapat dipilih?

Dengan aturan perkalian banyak menu yang dapat dipilih adalah:

Aturan Perkalian (Filling Slot)

5. Lea memiliki 3 baju yang berwarna Merah (M), Kuning (K) dan Putih (P). Selain itu ia juga memiliki celana yang berwarna Hitam (H) dan Coklat (C). Berapakah cara pemilihan pemasangan baju dan celana yang dapat digunakan oleh Lea?

Banyaknya cara pemilihan baju adalah 3 cara yaitu M, K dan P, sedangkan banyaknya cara pemilihan celana adalah 2 cara yaitu H dan C. Dengan demikian telah diketahui bahwa n1 = 3 dan n2 = 2.

Banyak cara pemilihan pasangan baju dan celana adalah 3 × 2 = 6.

Sedangkan pasangan baju dan celana tersebut adalah (1) MH, MC, (2) KH, KC, dan (3) PH, PC.

Itulah beberapa contoh soal aturan perkalian. Selamat mengerjakan.

Editor: Komaruddin Bagja

Pengaturan angka penting

Dilansir dari Khan Academy, angka penting adalah jumlah suatu nilai hasil pengukuran yang berkontribusi pada tingkat keakuratan nilai.

Sederhananya, angka penting adalah angka yang didapat dari hasil suatu pengukuran.

Baca juga: Pengukuran: Pengertian Para Ahli, Macam, Cara Penggunaan, dan Rumusnya

Angka penting terdiri dari angka pasti dan angka taksiran. Angka pasti adalah angka yang diperoleh dari skala alat ukur.

Sedangkan, angka taksiran adalah angka yang diperoleh dari satuan skala terkecil atau angka ketelitian alat ukur.

Penentuan angka penting memiliki aturan tertentu. Aturan angka penting adalah:

Baca juga: Bilangan yang Terdiri atas Tiga Angka yang Jumlahnya 9

Untuk lebih memahami tentang aturan angka penting, berikut adalah penjelasan dan contoh dari aturan angka penting!

Aturan Perhitungan Angka Penting

Berikut ketentuan perhitungan angka penting pada penjumlahan, pengurangan, perkalian, pembagian, pangkat, dan akar:

Cara Menghitung Penjumlahan, Pengurangan, Perkalian, Pembagian dalam Bentuk Pecahan

- Banyak sepatu yang dimiliki Tasya ada 2. Tasya dapat memilih salah satu dari 2 sepatu tersebut.

Oleh karena Tasyaharus memakai keduanya yaitu tas dan sepatu, banyak pilihan yang dimiliki Rani adalah 3 × 2 = 6.